Question

Sketch the graph of a continuous function f(x) satisfying the following properties: (i) the graph of f goes through the origin (ii) f0(−2) = 0 and f0(3) = 0. (iii) f0(x) > 0 on the intervals (−∞,−2) and (−2,3). (iv) f0(x) < 0 on the interval (3,∞). Label all important points.

Answer 1

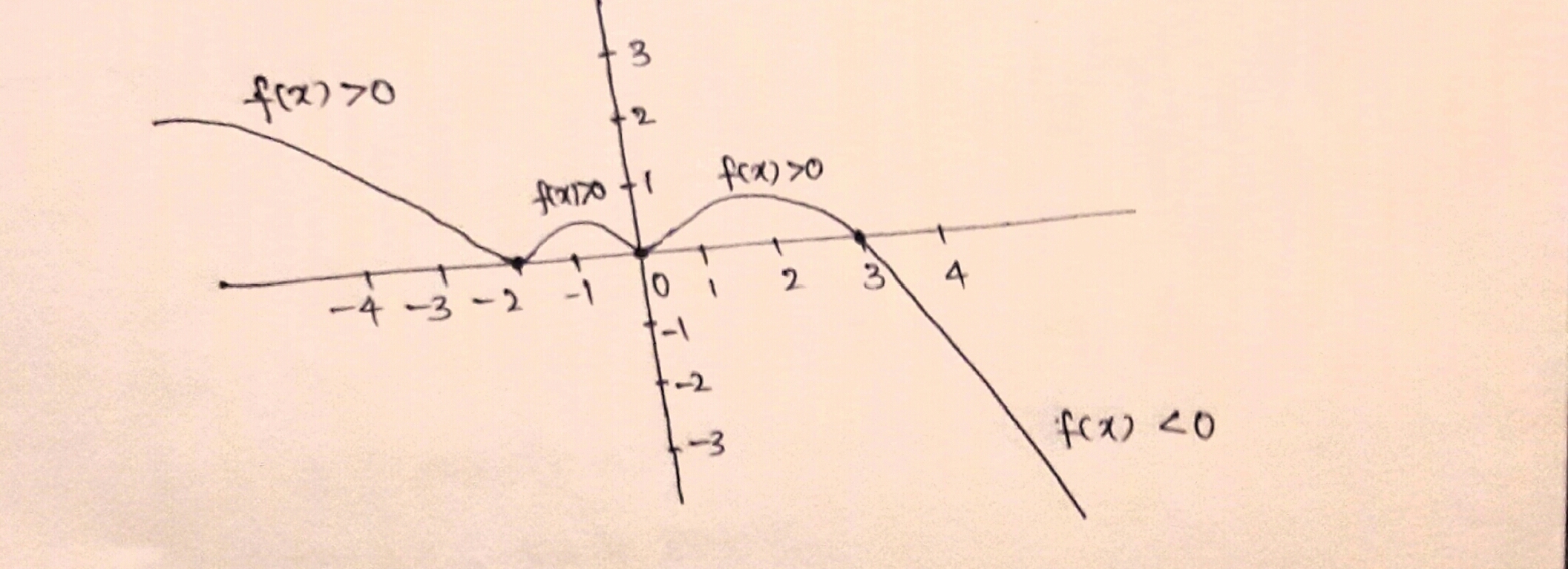
$i) f(x) \ goes \ through \ the \ origin\\ \Rightarrow (0,0) \ is \ a \ point \ on \ the \ curve.$

$ii) \ f(-2)=0 \ \\ \Rightarrow curve \ intersects \ x-axis\ at \ x=-2\\ iii) \ f(3)=0 \ \Rightarrow \ curve \ intersects \ x-Axis \ at \ x= 3 \\ \Rightarrow (3,0) \ is \ a \ point \ on \ the \ curve. \\ iv) f(x) > 0 \ in \ ({-\infty},-2)\ and \ (-2,3)\\ \Rightarrow f(x) \ is\ above \ the \ x-axis.\\ v) f(x) <0 \ in \ (3,{\infty}) \\ \Rightarrow f(x) \ is \ below \ the \ x-axis\\ Incorporating \ all \ the \ above \ properties \ the \ graph \ of \ the \ function \ is \ as \ follows:$