Question

A light on the ground at Lilys building is 30meters away from the building. Jade is 2 meters tall. She walks from the light to the building at 1 meters per second. How fast is the shadow of Jade on the building changing when she is 15 meters from the building.

Answer 1

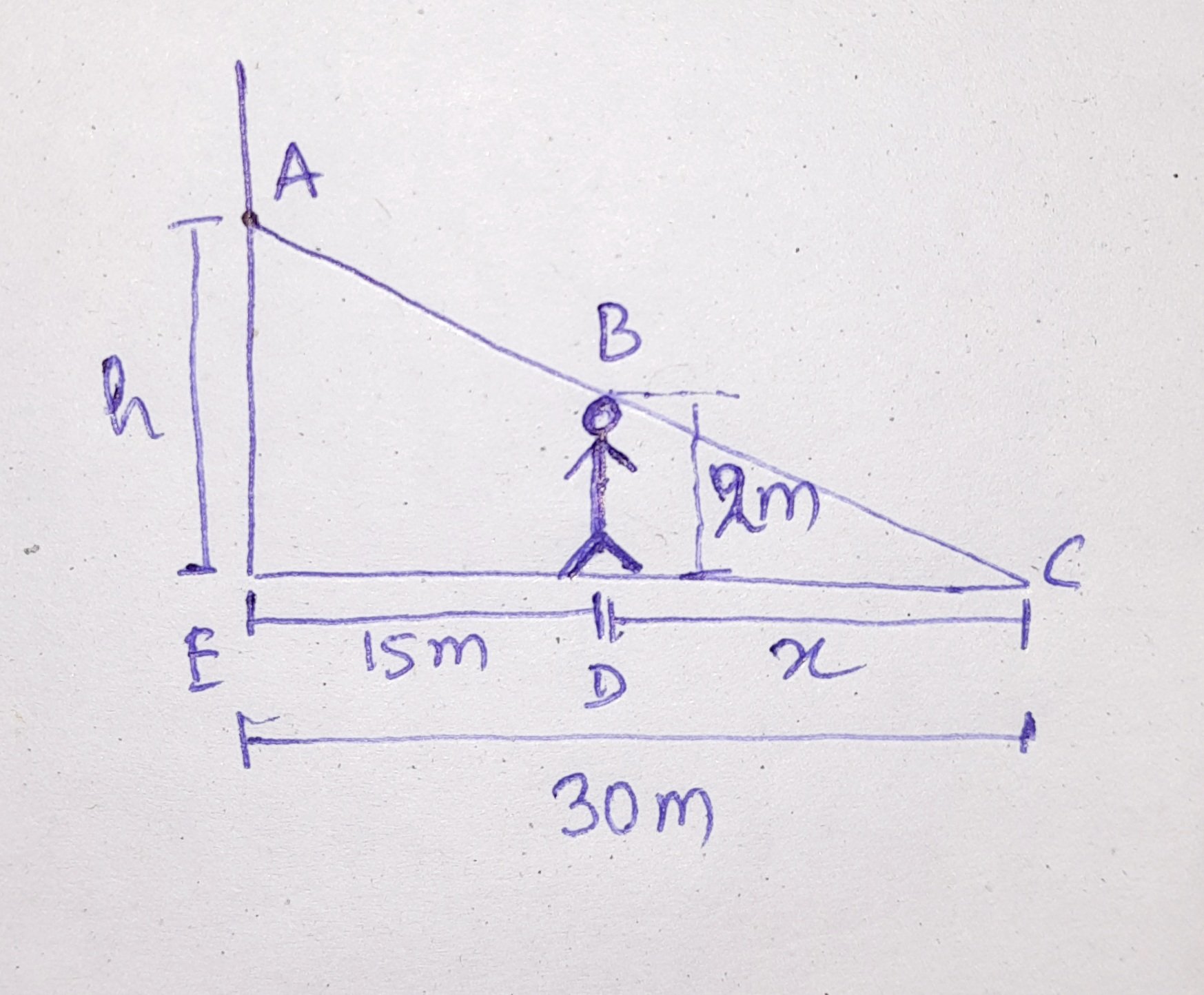
$\text{By using similar triangle property,}\newline \frac{2}{x}=\frac{h}{30}\newline h=\frac{60}{x}\newline \text{Differentiate wrt x,}\\ \frac{dh}{dx}=\frac{-60}{x^2}\\ Given, \frac{dx}{dt}=1m/sec.\newline \text{ we need to find} \frac{dh}{dt}.\newline Therefore, \frac{dh}{dt}=\frac{dh}{dx}× \frac{dx}{dt}\newline =\frac{-60}{x^2}×1\newline =\frac{-60}{x^2}\newline \text{ Given, when she is 15 m from the building.} \newline \implies x=30-15=15m\newline Therefore,\newline \frac{dh}{dt}=\frac{-60}{15^2}=\frac{-4}{15}=-0.267m/sec$