(1)y1=5x3+0x2+x+7&y2=5x4+0x2+1(2)I choose x = 3(3)If3is a zero ofy2,thenx - 3would be a factor ofy2,which implies that the binomial to be dividedbyy2to give a remainderis x - 3.(5)The remainder is145(6)No, my integer from part bis not a zero of my polynomial,because the remainder after the long division is not equal to0.
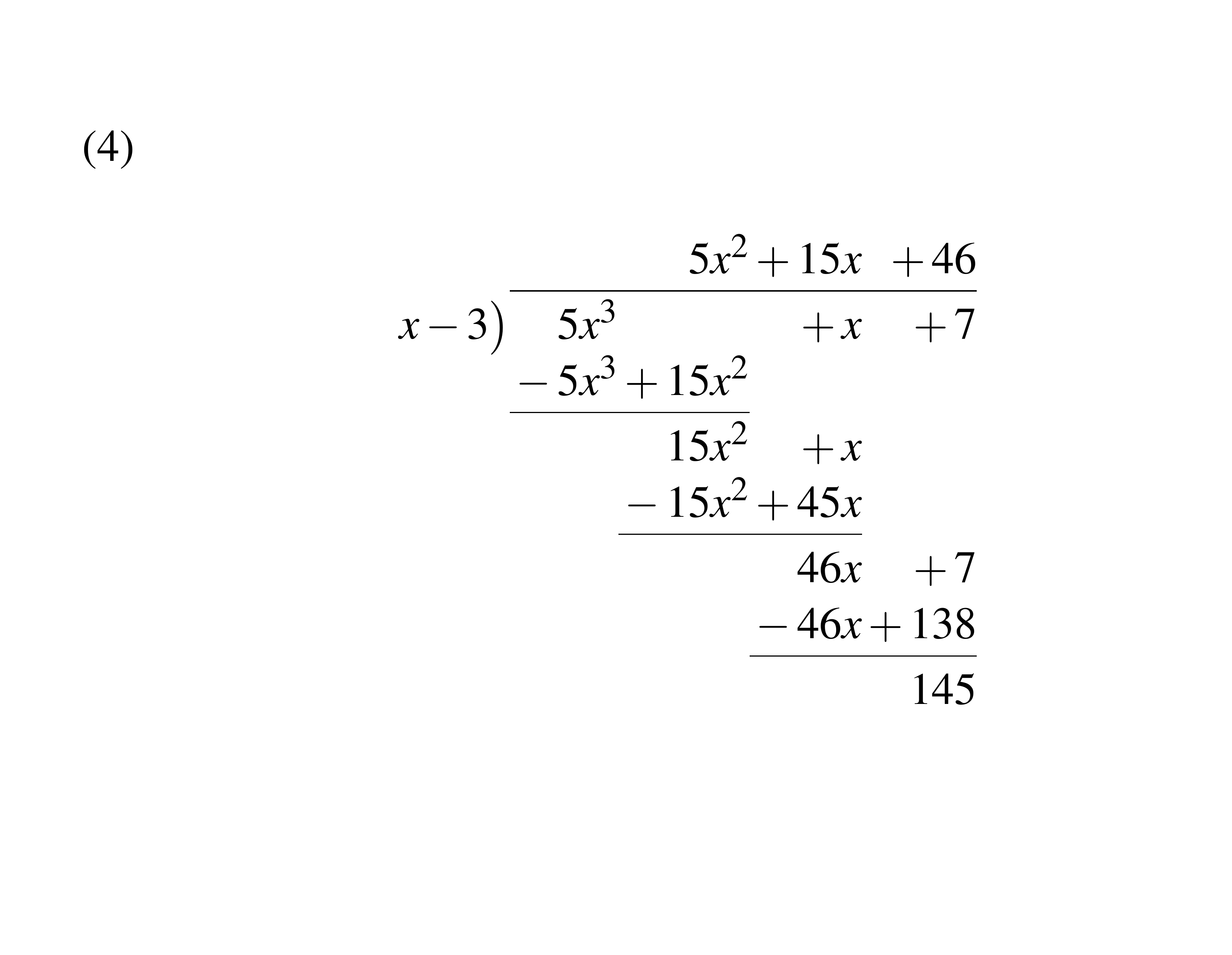


Comments