Question

1. Find R R
D
(x + 2y)dA, where D is the region bounded by the parabolas
y = x
2
, and y = 1 + x

Answer 1

$exact \space question\\ evaluate \space \int \space \int_{D} \space (x+2y)dA\\ where \space D \space is \space the \space region \space bounded \space by \space the \space parabolas \space y=2x^2 \space and \space y=1+x^2\\ ------------------------\\ solution\\ diagram\\:- where \space blue \space line \space represent \space y=2x^2\\ \space red \space line \space represent \space y=1+x^2$

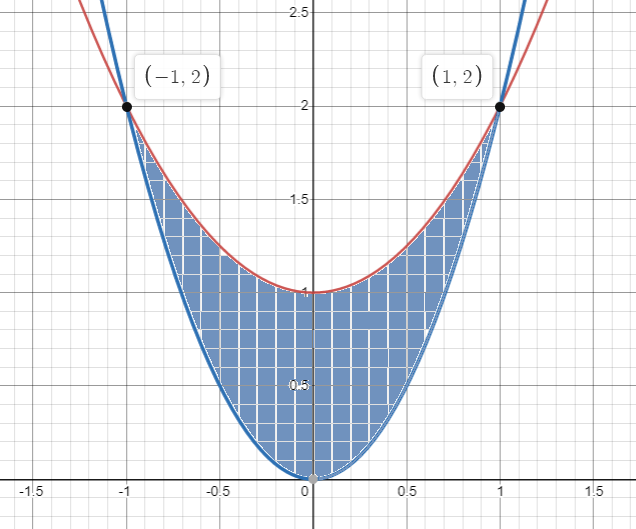
$\int \space \int_{D} \space (x+2y)dA=\int_{-1}^1 \space \int_{2x^2}^{1+x^2}(x+2y)dydx\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space =\int_{-1}^1 \space (xy+y^2)|_{2x^2}^{1+x^2}dx\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space =\int_{-1}^1[(x(1+x^2)+(1+x^2)^2)-(x(2x^2)+(2x^2)^2)]dx\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space =\int_{-1}^1[(x+x^3+1+2x^2+x^4)-(2x^3+4x^4)]dx\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space =\int_{-1}^1[(1+x+2x^2-x^3-3x^4)]dx\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space =[x+\frac{x^2}{2}+\frac{2x^3}{3}-\frac{x^4}{4}-\frac{3x^5}{5}]_{-1}^1\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space =\frac{32}{15}\\ hence \space required \space solution=\frac{32}{15}\\$