Consider the given region :
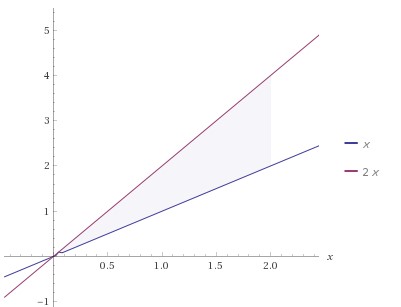
The given region isx≤y≤2x0≤x≤2Find the integral as0∫2x∫2x(x4+y2)dydx=0∫2[x4y+3y3]x2xdx=0∫2((x4(2x)+3(2x)3)−(x4(x)+3(x)3))dx=0∫2((2x5+38x3)−(x5+3x3))dx=0∫2(x5+37x3)dxApplythePowerRule:∫xadx=a+1xa+1=[6x6+127x4]02=626+127⋅24−0=20


Comments
Dear Pintoo, please use the panel for submitting new questions.
Find the range of the function f defined by f(x y)=10-x^2-y^2 for all (x y) for which x^2+y^2