Question

the angle of elevation to the top of a 10 story skyscraper is measured to be 3 degrees from a point on the ground 2,000 feet from the building. what is the height of the skyscraper to the nearest hundreth foot.

Answer 1

A representation of the above question is shown below:

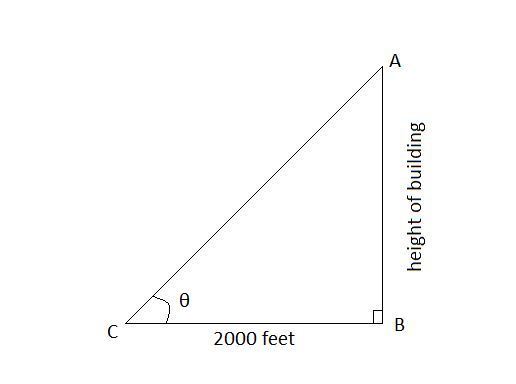
$\begin{aligned} &\text { Angle of elevation, } \theta=3 \degree \\ &\text { Distance between building and observing point }=2000 \text { feet } \\ &\Rightarrow \mathrm{BC}=2000 \text { feet } \\ &\text { To find : Height of the building, } \mathrm{AB} \\ &\text { Since, the building and the ground surface are perpendicular to each other } \\ &\Rightarrow \triangle \mathrm{ABC} \text { is a right angle triangle right angled at } \mathrm{B} \\ &\text { Now, to find height of building using property of tan in } \triangle \mathrm{ABC} \\ &\tan \theta =\frac{\text { Perpendicular }}{B a s e} \\ &\tan 3 \degree=\frac{A B}{2000} \\ &\Longrightarrow 0.0524=\frac{A B}{2000} \\ &\Longrightarrow A B=2000 \times 0.0524 \\ &\Longrightarrow \mathrm{AB}=104.8 \text { feet } \\ &\text { Hence, The height of the building }=104.8 \text { feet } \\ \end{aligned}$