Question

a car travels 32km due north and then 46 km in a direction 40 degrees west of north. find the direction of the car's resultant vector

Answer 1

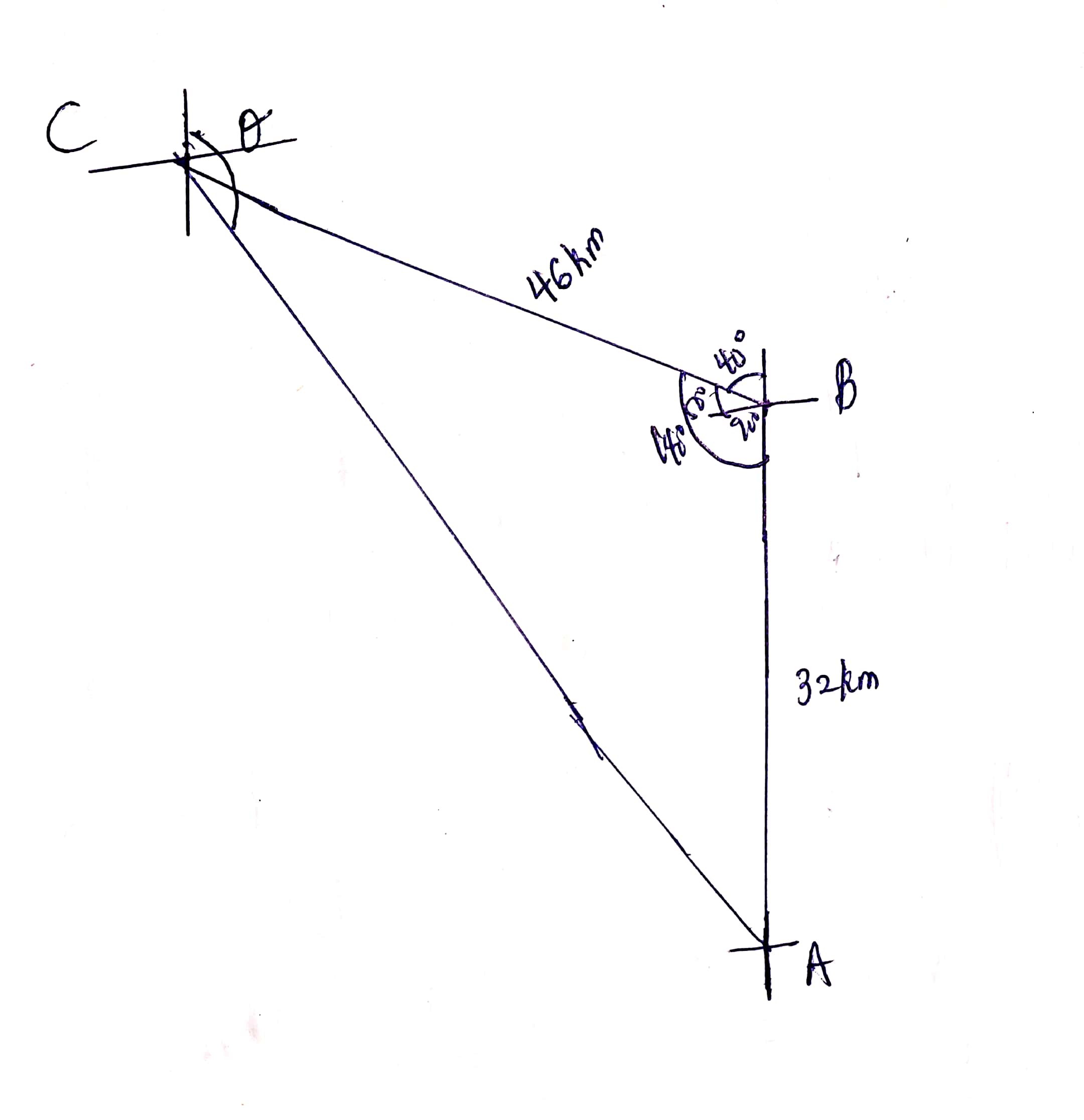
$\textsf{If} \hspace{0.1cm}a, b\hspace{0.1cm} \textsf{and}\hspace{0.1cm} c \hspace{0.1cm}\textsf{are the}\\\textsf{sides opposite to angles} \hspace{0.1cm}A, B,\hspace{0.1cm}\&\hspace{0.1cm}C.\\ \textsf{By Cosine Rule,}\\ b^2 = 32^2 + 46^2 - (2 \times 32 \times 46\cos{140\degree})\\ b^2 = 1024 + 2116 - 2944\cos{140\degree}\\ b^2 = 3140 - 2944\cos{140\degree} \\ b^2 = 3140 + 2255.234841 \\ b^2 = 5395.234841 \\ b = 73.45\\ \textsf{By Sine Rule,}\\ \frac{32}{\sin{C}} = \frac{73.45}{\sin{140\degree}}\\ \sin{C} = \frac{32\sin{140\degree}}{73.45}\\ \sin{C} = 0.2800\\ C = 16.26\degree\\ \textsf{The direction of the resultant}\\\textsf{vector is measured from}\hspace{0.1cm}0\degree\hspace{0.1cm} \textsf{east}\\\textsf{to the resultant, this angle is} \hspace{0.1cm} \theta - 90\degree,\\\hspace{0.1cm} 90\degree \textsf{is the total angle in}\\\textsf{ the first quadrant.}\\ \therefore\theta - 90\degree = C + \phi\\ \phi = 50\degree \hspace{0.1cm} \{\textsf{Alternate angles are equal}\}\\ \therefore\textsf{The direction of the car's}\\\textsf{resultant vector is}\hspace{0.1cm} 50\degree + 16.26 \degree = 66.26\degree \hspace{0.1cm}\textsf{south of east}$