Answer to Question #125770 in Statistics and Probability for Christian

Question

The marketing director of GH HOTEL was interested in studying the intention of consumers
to visit their facility after the president has fully lifted the restriction on public gathering in
2020 and as a follow- up, whether they in fact actually visited. Suppose that a sample of 1000
household was initially selected and the respondents were asked whether they planned to visit
GH HOTEL. Twelve months later the same respondents were asked whether they actually
visited the hotel. The results are summarized in the table below
Planned to visit Yes No Total
Yes 200 50 250
No 100 650 750
Total 300 700 1000
i. Draw a tree diagram to represent the information in the table.
ii. Find the probability of selecting a respondent who actually visited GH HOTEL.
Interpret your answer in a simple single sentence.
iii. Find the probability of panned visit or actual visit.
iv. Calculate the probability that a respondent actually visited GH HOTEL given that he
or she planned to visit GH HOTEL.

Answer 1

$$\def\arraystretch{1.5} \begin{array}{c:c:} & & Planned & to & visit \\ & & Yes & No & Total \\ \hline & Yes & 200 & 50 & 250 \\ \hdashline Visited & No & 100 & 650 & 750 \\ \hdashline & Total & 300 & 700 & 1000 \end{array}$$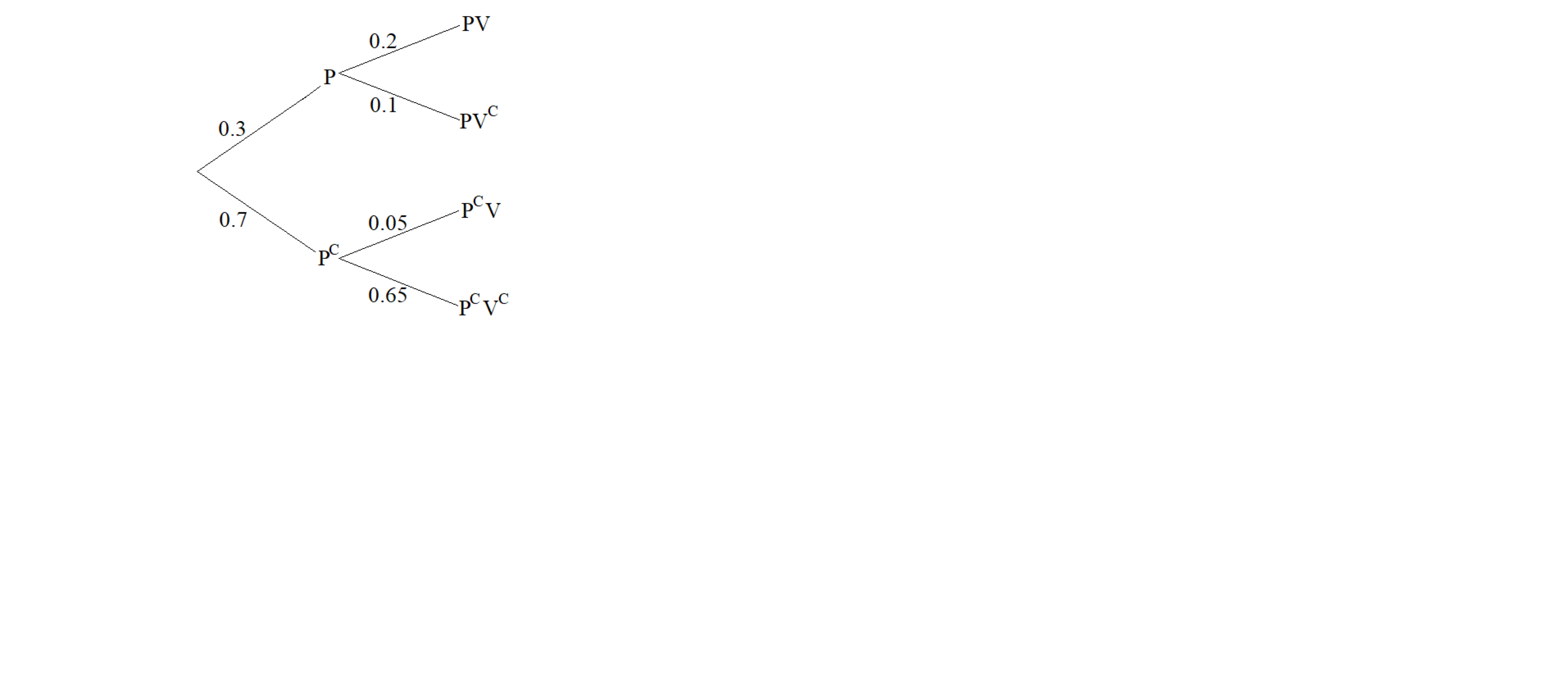

i. Draw a tree diagram to represent the information in the table.

ii. Find the probability of selecting a respondent who actually visited GH HOTEL.

$$P(V)=P(PV)+P(P^CV)=0.2+0.05=0.25$$

Tne number of people actually visited GH HOTEL equals to the number of people who planned and visited plus the number of people who no planned but visited.

iii. Find the probability of planned visit or actual visit.

$$P(P\cup V)=P(P)+P(V)-P(P V)=$$ $$=0.3+0.25-0.2=0.35=$$ $$=1-P(P^CV^C)=1-0.65=0.35$$

Tne number of people planned visit or visited equals the total number of people minus the number of people who no planned and no visited.

iv. Calculate the probability that a respondent actually visited GH HOTEL given that he

or she planned to visit GH HOTEL.

Conditional probability

$$P(V|P)=\dfrac{P(PV)}{P(V)}=\dfrac{0.2}{0.25}=0.8$$