ANSWER ∫∫∫E 6z2dV= 4625=156.25
EXPLANATION
The projection of the set E={(x,y,z):0≤x≤25,0≤y≤5−2x,0≤z≤5−2x−y}
onto the x0y plane is the region
D={(x,y):0≤x≤25,0≤y≤5−2x}.
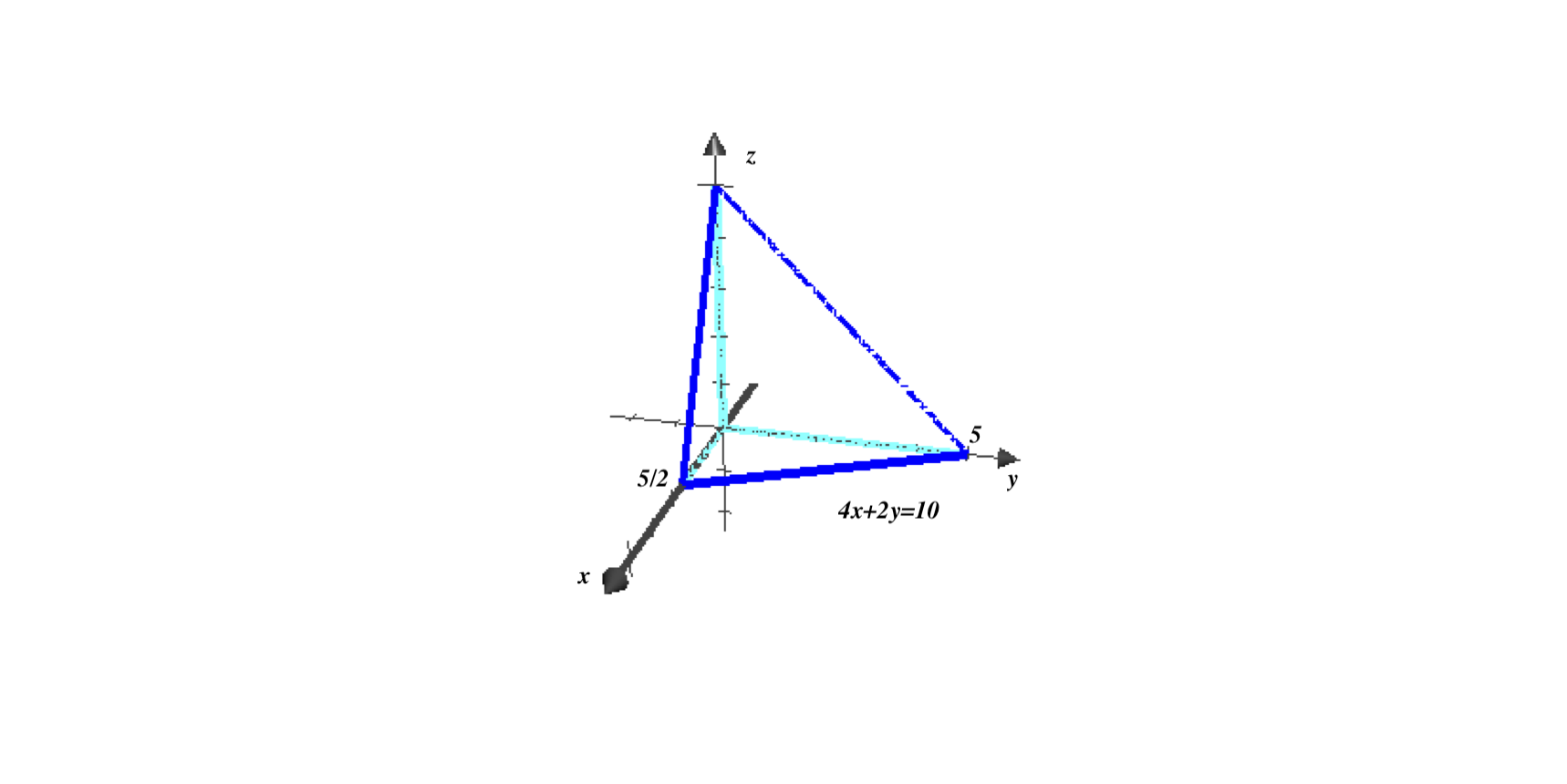
∫∫∫E 6z2dV=∫025∫05−2x∫05−2x−y6z2dzdydx=6∫025∫05−2x[3z3]05−2x−ydydx=2∫025∫05−2x(5−2x−y)3dydx=2∫025[−4(5−2x−y)4]y=0y=5−2xdx==21∫025(5−2x)4dx=21[−10(5−2x)5]025=2055=4625=156.25


Comments