Question

Find the absolute minimum of the function f(x, y) = 3 +xy-x-2yon the closed triangular region with vertices (1,0), (5,0), and (1,4).

Answer 1

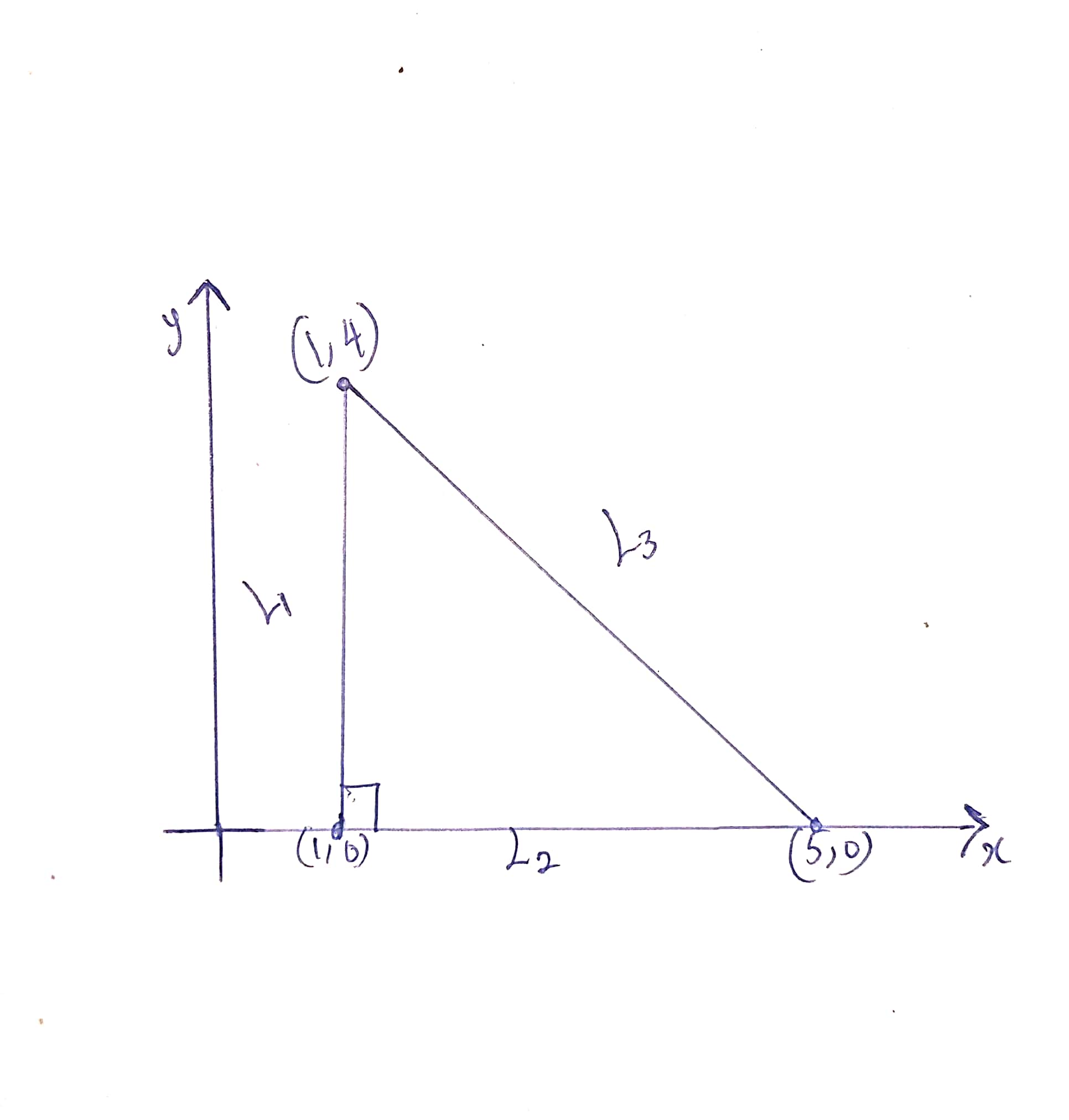
$\displaystyle\textsf{Since}\, f \, \textsf{is a polynomial, it is continuous on the closed,}\\ \textsf{bounded set}\, T,\, \textsf{where}\, T\, \textsf{is the region in the triangle.} \\ \textsf{The first order partial derivatives are} \\ f_x(x, y) = y - 1\, \textsf{and}\, f_y(x, y) = x - 2 \\ \textsf{Thus, the only critical points in the interior of} \,T\,\textsf{is} \,(2, 1) \\ \textsf{The boundary of}\,T \, \textsf{consists of three line segments,}\\ L_1, L_2 \, \textsf{and} L_3. \\ \textsf{On}\, L_1,\, \textsf{we have}\, x = 1, \\ f(1, y) = 3 + y - 1 - 2y = 2 - y \\ \textsf{The function}\, f \, \textsf{is a decreasing function of}\,y \\ \textsf{along}\, L_1 \, \textsf{from}\, (1, 0) \, \textsf{to}\, (1, 4)\\ \textsf{Its maximum value is}\, f(1, 0)\, \textsf{and its minimum value is}\,f(1, 4) \\ \textsf{On}\, L_2, \, \textsf{we have} \,y = 0, \\ f(1, y) = 3 - x\\ \textsf{The function}\, f\, \textsf{is a decreasing function of}\, x \textsf{along}\\ L_2\, \textsf{from} (1, 0)\, \textsf{to}\,(5, 0) \\ \textsf{Its maximum value is}\, f(1, 0)\, \textsf{and its minimum value is}\, f(5, 0) \\ \textsf{Deriving an equation for line}\, L_3\\ \textsf{The equation can be derived}\\\textsf{from the formula for the equation}\\ \textsf{of a straight line passing through}\\ \textsf{one point with a gradient which is given by} \\ \frac{y - y_1}{x - x_1} = m(x - x_1) \\ \textsf{since the line is passing through}\, (1, 4) \, \textsf{and}\, (5, 0) \\ m = \frac{0 - 4}{5 - 1} = \frac{-4}{4} = -1 \\ \frac{y - 0}{x - 5} = -1 \\ \therefore y = 5 - x \\ f(x, 5 - x) = 3 + x(5 - x - 1) - 2(5 - x) \\ f(x, 5 - x) = 3 + 4x - x^2 - 10 + 2x = 6x - x^2 - 7 \\ f_x(x, 5 - x) = 6 - 2x = 0, \implies x = 3\, \textsf{and so},\, (3, 2)\, \textsf{is a critical point.} \\ \textsf{The values of the function at the}\\\textsf{critical points is given by;}\\ \begin{aligned} f(3, 2) &= 3 + 3(2 - 1) - 2(3) = 0 \\ f(1, 0) &= 3 - 1 = 2\\ f(5, 0) &= 3 - 5 = -2\\ f(1, 4) &= 3 + 1(4 - 1) - 2(4) = -2\\ f(2, 1) &= 3 + 2(1 - 1) - 2(1) = 1 \end{aligned} \\ \textsf{We can hence conclude that}\, -2\, \textsf{is the absolute }\\ \textsf{minimum of the function}\, f(x, y) = 3 + x(y - 1) - 2y\, \textsf{on the closed}\\ \textsf{triangular region with vertices}\, (1,0), (5, 0) \,\textsf{and}\, (1, 4).$