Question

Assuming you are a researcher tasked to know about some truths in life. You plan to investigate
the growth or decay of some things that interest you. You are to report what you have researched
and present exponential or logarithmic functions that would model the involved quantities. You
also have to present the graph and explain its characteristics or behavior.

Answer 1

$\displaystyle \textbf{Modeling population growth and decay rates}\\ \textsf{To understand the different models}\\ \textsf{that are used to represent population}\\ \textsf{dynamics, let's start by looking at a}\\ \textsf{general equation for the population growth}\\ \textsf{rate (change in number of individuals}\\ \textsf{in a population over time):}\\ \frac{\mathrm{d}N}{\mathrm{d}t} = rN\\ \textsf{is the growth rate of the population}\\ \textsf{in a given instant,}\, N\,\textsf{is population}\\ \textsf{size,}\,t\, \textsf{is time, and} \\ r\, \textsf{is the per capita rate of increase}\\ \textsf{that is, how quickly the population}\\ \textsf{grows per individual already in the}\\ \textsf{population.}\\ \textsf{If we assume no movement of individuals}\\ \textsf{into or out of the population is,}\,r\\ \textsf{just a function of birth and death rates.}\\$

$\textbf{Derivation of the solution to the differential equation}\\$

$\dfrac{\mathrm{d}N}{\mathrm{d}t} = rN\\$

$\dfrac{\mathrm{d}N}{N} = r\, \mathrm{d}t$

$\\ \int\,\dfrac{\mathrm{d}N}{N} = \int\,r\, \mathrm{d}t\\$

$\ln(N) = rt + C\\ N = Ae^{rt}\\$

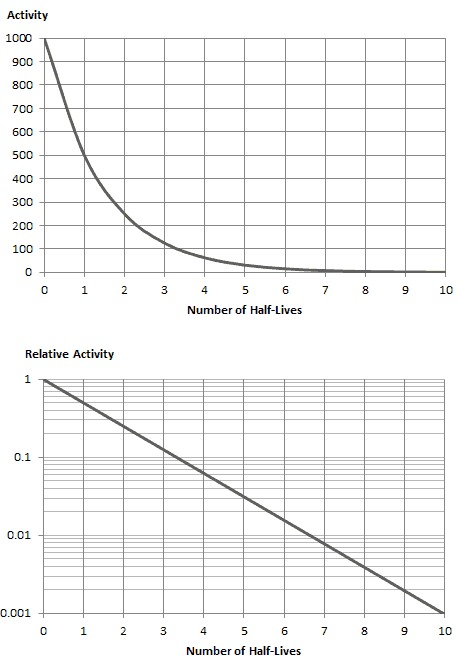
Therefore this means that the growth and decay of some materials increases exponentially as the time increases