Answer to Question #252498 in Mechanics | Relativity for Neil

Question

The portion of a bridge truss is subjected tp several loads for the loading shown, determine the location in the x-2 plane through which the resultant passed.

Answer 1

Let use the following example

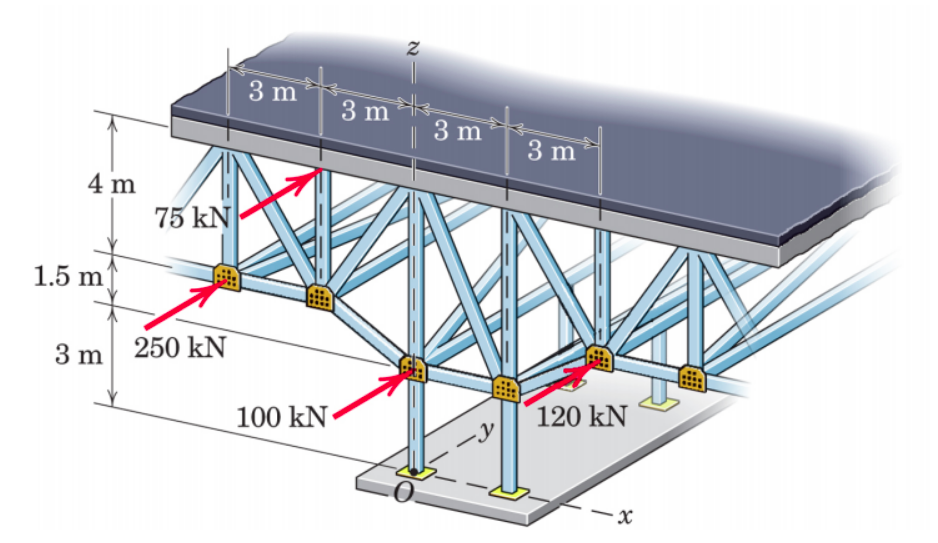
$P_1 = 250 \;kN \\ x_1 = -3 \;m \times 2 = -6 \;m \\ z_1 = 3 \;m + 1.5 \;m = 4.5 \;m \\ (-6\;m, 4.5\;m) \\ P_2 = 75 \;kN \\ x_2 = -3 \;m \\ z_2 = 3 \; + 1.5 \;m +4 \; m= 8.5 \;m \\ (-3\; m, 8.5\; m) \\ P_3 = 100 \;kN \\ x_3 = 0 \;m \\ z_3 = 3 \;m \\ (0\;m, 3\; m) \\ P_4 = 120 \;kN \\ x_4 = 3 \; m \times 2 = 6 \;m \\ z_4 = 3 \; m + 1.5 \;m = 4.5 \;m \\ (6\; m, 4.5\; m) \\ R=P1 +P_2 +P_3 +P_4 \\ = 250 \;kN + 75 \;kN + 100 \;kN +120 \;kN = 545 \;kN \\ x_R = \frac{P_1x_1 + P_2x_2 + P_3x_3 +P_4x_4}{R} \\ = \frac{250 \times (-6) + 75 \times (-3) + 100 \times 0 + 120 \times 6}{545} \\ = \frac{-1005}{545} \\ = -1.844 \;m \\ z_R = \frac{P_1z_1 + P_2z_2 + P_3z_3 +P_4 z_4}{R} \\ = \frac{250 \times 4.5 + 75 \times 8.5 + 100 \times 3 +120 \times 4.5}{545} \\ = \frac{2602.5}{545} \\ = 4.775 \;m \\ (x_r, z_R) = (-1.844 \;m, 4.775 \;m)$