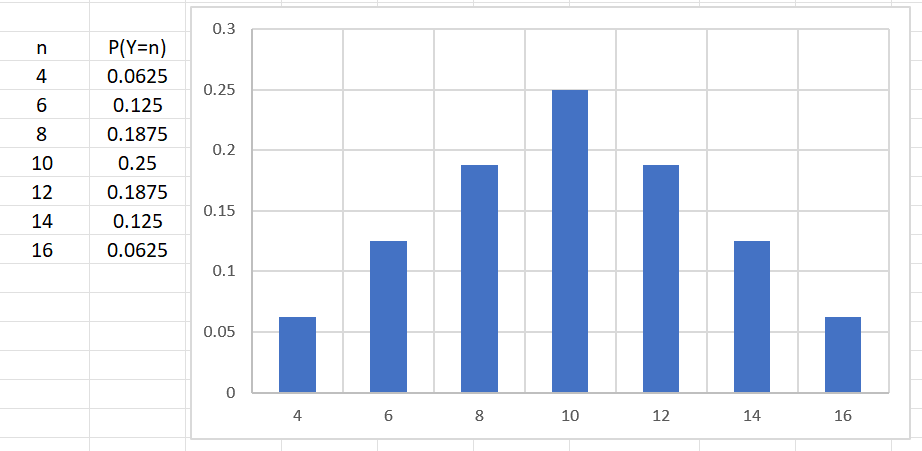
Y=X1+X2P(Y=4)=P(2,2)=41⋅41=0.0625P(Y=6)=P(2,4)+P(4,2)=41⋅41+41⋅41=0.125P(Y=8)=P(2,6)+P(4,4)+P(6,2)=41⋅41+41⋅41+41⋅41=0.1875P(Y=10)=P(2,8)+P(4,6)+P(6,4)+P(8,2)=41⋅41+41⋅41+41⋅41+41⋅41=0.25P(Y=12)=P(4,8)+P(6,6)+P(8,4)=41⋅41+41⋅41+41⋅41=0.1875P(Y=14)=P(6,8)+P(8,6)=41⋅41+41⋅41=0.125P(Y=16)=P(8,8)=41⋅41=0.0625


Comments