Answer to Question #225846 in Operations Research for mafi

Question

Hint:Solve the below formulated LPM using Graphics method.

Z-Min = 1500x+2400y

Subjected to:

4x+Y>24

2x+3y>42

X+4y>36

X<14

Y<14

X, y>0 Required: Perform the below requirements by Using the Graphics method through considering

appropriate steps and procedures.

i. Solve using Graphics method?

Answer 1

$solution\\ given \space problem \space \\ MIN \space Z_x = 1500 x_1 + 2400 x_2\\ subject \space to\\ 4 x_1 + x_2 ≥ 24\\ 2 x_1 + 3 x_2 ≥ 42\\ x_1 + 4 x_2 ≥ 36\\ x_1 ≤ 14\\ x_2 ≤ 14\\ and \space x_1,x_2≥0;\\ ----------------------\\ (1). \space To \space draw \space constraint \space 4x_1+x_2≥24 → (1)\\ Treat \space it \space as \space 4x_1+x_2=24\\ When \space x_1=0 \space then \space x_2= ? \\ ⇒4(0)+x_2=24\\ ⇒x_2=24\\ When \space x_2=0 \space then \space x_1= ? \\ ⇒4x_1+(0)=24\\ ⇒4x_1=24\\ =x_1=6\\ \begin{vmatrix}x_1 & \space 0 & \space 6\\ x_2 & \space 24 \space & \space 0 \end{vmatrix}\\ ----------------------\\ similar\\ (2).To \space draw \space constraint \space 2x_1+3x_2≥42→(2)\\ \begin{vmatrix}x_1 & \space 0 & \space 21\\ x_2 & \space 14& \space 0 \end{vmatrix}\\ ----------------------\\ (3)To \space draw \space constraint \space x_1+4x_2≥36→(3)\\ \begin{vmatrix}x_1 & \space 0 & \space 36\\ x_2 & \space 9& \space 0 \end{vmatrix}\\ ----------------------\\ (4) \space To \space draw \space constraint \space x_1≤14→(4)\\ \begin{vmatrix}x_1 & \space 14 & \space 14\\ x_2 & \space 0 \space & \space 1 \end{vmatrix}\\ ----------------------\\ (5)To \space draw \space constraint \space x_2≤14→(5)\\ \begin{vmatrix}x_1 & \space 0 & \space 1\\ x_2 & \space 14 \space & \space 14 \end{vmatrix}\\ ----------------------\\ now \space we \space draw \space graph \space of \space above \space 1 \space to \space 5 \space data \space set. \\ \space graph \space \\$

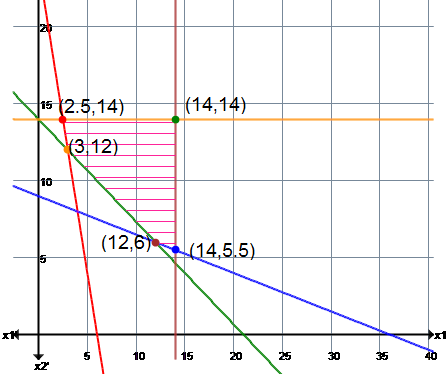
$yellow \space line \space \space x_2≤14\\ brown \space line \space x_1≤14\\ blue \space line \space x_1+4x_2≥36\\ green \space line \space 2x_1+3x_2≥42\\ red \space line \space 4x_1+x_2≥24\\ ----------------------\\ The \space value \space of \space the \space objective \space function \space at \space each \space of \space these \space extreme \space points \space is \space as \space follows:\\ \begin{vmatrix} Extreme \space Point Coordinates (x_1,x_2) \space & \space Objective \space function \space value Z=1500x_1+2400x_2 \space \\ A(2.5,14) & 1500(2.5)+2400(14)=37350\\ B(14,14) & 1500(14)+2400(14)=54600\\ C(14,5.5) & 1500(14)+2400(5.5)=34200\\ D(12,6) & 1500(12)+2400(6)=32400\\ E(3,12) & 1500(3)+2400(12)=33300\\ \end{vmatrix}\\ The \space miniimum \space value \space of \space the \space objective \space function \space Z=32400 \space occurs \space at \space the \space extreme \space point \space (12,6).\\ Hence, \space the \space optimal \space solution \space to \space the \space given \space LP \space problem \space is \space : \space x_1=12,x_2=6 \space and \space min \space Z=32400.\\$