Answer to Question #222591 in Operations Research for HANNA

Question

Problem 1: A farmer plans to mix two types of food to make a mix of low cost feed

for the animals in his farm. A bag of food A costs $10 and contains 40 units of

proteins, 20 units of minerals and 10 units of vitamins. A bag of food B costs $12

and contains 30 units of proteins, 20 units of minerals and 30 units of vitamins. How

many bags of food A and B should the consumed by the animals each day in order to

meet the minimum daily requirements of 150 units of proteins, 90 units of minerals

and 60 units of vitamins at a minimum cost?

A. Formulate the problem in to linear programming problem model

B. Use graphical approach to find the solution

Answer 1

Let $x \ \text{and} \ y$ be the number of beg $A$ and $B$ respectively to meet the minimum daily requirements of food.

Then according to question,

(A)'Formulate the problem in to linear programming problem model'

Minimize ,$Z=10x_1+12x_2$

Subject to ,$40x_1+30x_2\ge150$

$20x_1+20x_2\geq90$

$10x_1+30x_2\ge60,x_1\geq0,x_2\ge0.$

(B). Use graphical approach to find the solution

$1. \space To \space draw \space constraint \space 40x_1+30x_2≥150→(1) \\ \\ Treat \space it \space as \space 40x_1+30x_2=150 \\ (RED \space LINE \space IN \space GRAPH) \\ \\ x_1 \space \space \space \space \space \space 0 \space \space \space \space \space \space 3.75 \\ x_2 \space \space \space \space \space \space 5 \space \space \space \space \space \space 0 \\ \\ 2. \space To \space draw \space constraint \space 20x_1+20x_2≥90→(2) \\ \\ Treat \space it \space as \space 20x_1+20x_2=90 \\ (GREEN \space LINE \space IN \space GRAPH) \\ \\ x_1 \space \space \space \space \space \space 0 \space \space \space \space \space \space 4.5 \\ x_2 \space \space \space \space \space \space 4.5 \space \space \space \space \space \space 0 \\ \\ 3. \space To \space draw \space constraint \space 10x_1+30x_2≥60→(3) \\ \\ Treat \space it \space as \space 10x_1+30x_2=60 \\ (BLACK \space LINE \space IN \space GRAPH) \\ \\ x_1 \space \space \space \space \space \space 0 \space \space \space \space \space \space 6 \\ x_2 \space \space \space \space \space \space 2 \space \space \space \space \space \space 0 \\$

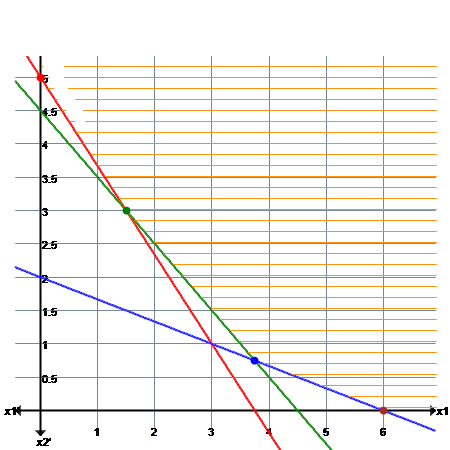
The value of the objective function at each of these extreme points is as follows:

Extreme Point Objective function value

Coordinates $Z=10x_1+12x_2$

A(0,5) 10(0)+12(5)=60

B(1.5,3) 10(1.5)+12(3)=51

C(3.75,0.75) 10(3.75)+12(0.75)=46.5

D(6,0) 10(6)+12(0)=60

The minimum value of the objective function Z=46.5 occurs at the extreme point (3.75,0.75).

Hence, the optimal solution to the given LP problem is : $x_1$ =3.75, $x_2$ =0.75 and min Z=46.5.