Answer to Question #223684 in Statistics and Probability for Khalid

Question

From a box containing 5 dimes and 3 nickels, 4 coins are selected at random without replacement.

Find the probability distribution for the total T of the 4 coins. Express the probability distribution graphically as a probability histogram. Find the Expected Value and Standard Deviation of the number of coins.

Answer 1

$$P(4D \& 0N)=\dfrac{\dbinom{5}{4}\dbinom{3}{0}}{\dbinom{5+3}{4}}=\dfrac{1}{14}$$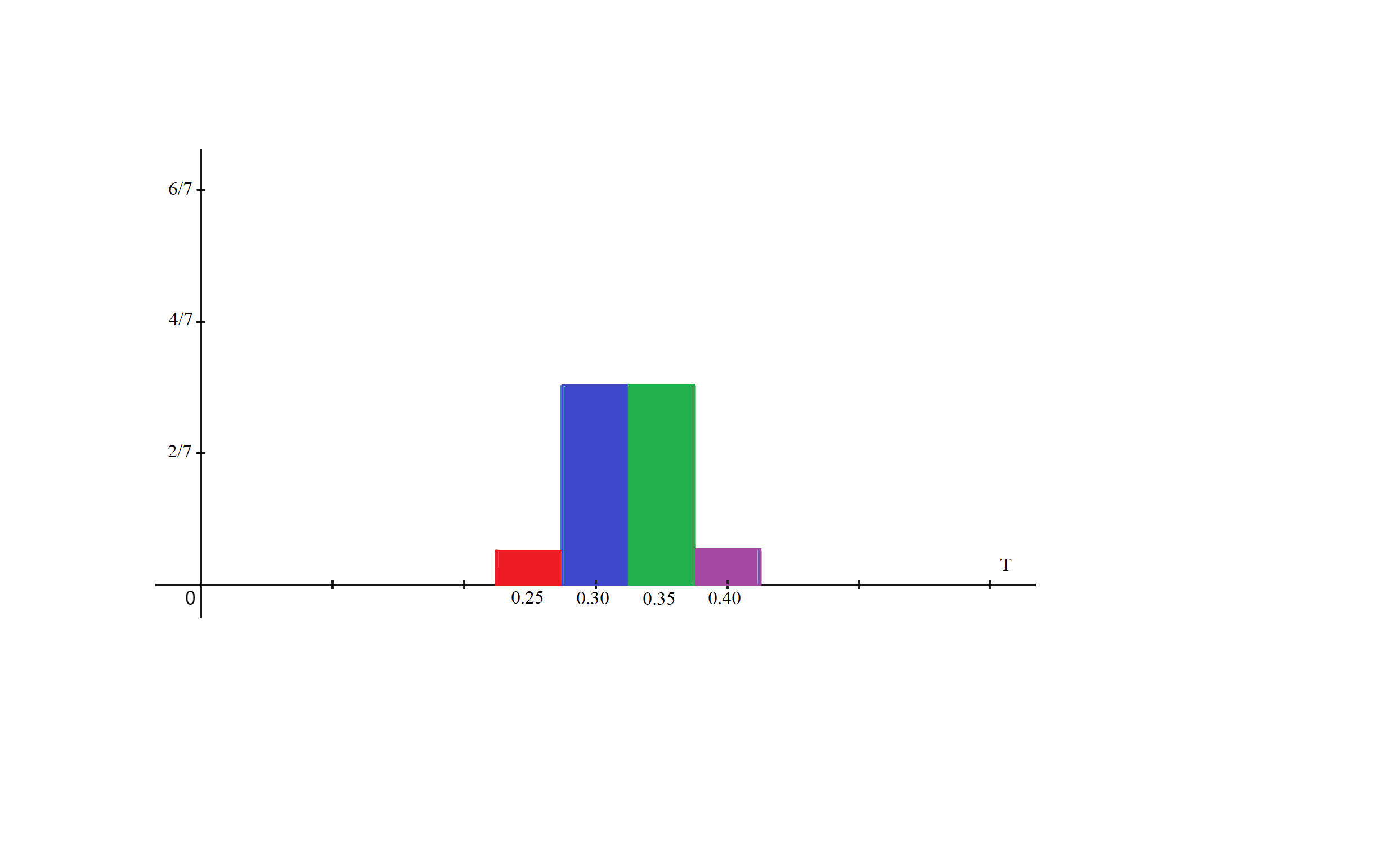

$$P(3D \& 1N)=\dfrac{\dbinom{5}{3}\dbinom{3}{1}}{\dbinom{5+3}{4}}=\dfrac{3}{7}$$

$$P(2D \& 2N)=\dfrac{\dbinom{5}{2}\dbinom{3}{2}}{\dbinom{5+3}{4}}=\dfrac{3}{7}$$

$$P(1D \& 3N)=\dfrac{\dbinom{5}{1}\dbinom{3}{3}}{\dbinom{5+3}{4}}=\dfrac{1}{14}$$

$$\begin{matrix} T & 0.40 & 0.35 & 0.30 & 0.25\\ \\ p(T) & \dfrac{1}{14} & \dfrac{3}{7} & \dfrac{3}{7}& \dfrac{1}{14} \end{matrix}$$

$$E(T)=\dfrac{1}{14}(0.40)+\dfrac{3}{7}(0.35)+\dfrac{3}{7}(0.30)+\dfrac{1}{14}(0.25)$$

$$=0.325$$

$$E(T^2)=\dfrac{1}{14}(0.40)^2+\dfrac{3}{7}(0.35)^2+\dfrac{3}{7}(0.30)^2$$

$$+\dfrac{1}{14}(0.25)^2=\dfrac{1.4975}{14}$$

$$Var(T)=\sigma^2=E(T^2)-(E(T))^2$$

$$=\dfrac{1.4975}{14}-(0.325)^2\approx0.001339$$

$$\sigma=\sqrt{\sigma^2}\approx\sqrt{0.001339}\approx0.0366$$