Answer to Question #283401 in Operations Research for Andinet

Question

7. A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for at least 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1unit of each of M & N on the three machines are given in following table

Items Numbers of hours required on machines

I II III

M 1 2 1

N 2 1 1.25

She makes a profit of Birr 600 and Birr 400 on items M and N respectively. How many

of each item should she produce so as to maximize her profit assuming that she can sell

all the items that she produced? What will be the maximum profit? (Solve through simplex method)

Answer 1

$\begin{aligned} &\text { Let } x \text { and } y \text { be the number of items } M \text { and } N \text { respectively. } \\ &\text { Total profit on the production }=\text { Rs }(600 x+400 y) \\ &\text { Mathematical formulation of the given problem is as follows: } \\ &\text { Maximise } Z=600 x+400 y \\ &\text { subject to the constraints: } \\ &x+2 y \leq 12 \text { (constraint on Machine I) ... (1) } \\ &2 x+y \leq 12 \text { (constraint on Machine II) ... (2) } \\ &x+5 / 4 y \geq 5 \text { (constraint on Machine III) ... (3) } \\ &x \geq 0, y \geq 0 \text {... (4) } \\ &\text { Let us draw the graph of constraints (1) to (4). ABCDE is the feasible region (shaded) } \\ &\text { as shown in below figure determined by the constraints (1) to (4). Observe that the } \\ &\text { feasible region is bounded, coordinates of the corner points A, B, C, D and E are (5, } \\ &0 \text { ) }(6,0),(4,4),(0,6) \text { and (0, 4) respectively. Let us evaluate Z = } 600 x+400 y \text { at } \\ &\text { these corner points. } \end{aligned}$

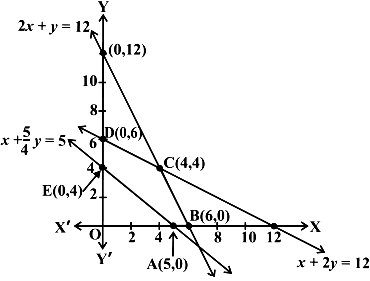
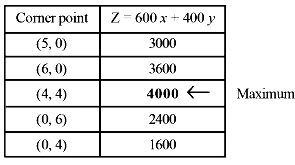
We see that the point (4, 4) is giving the maximum value of Z. Hence, the manufacturer has to produce 4 units of each item to get the maximum profit of Rs 4000.