optimization problem is
primal problem
maximize 90x+110ysubject to,2x+4y≤7000x+2.5y≤40002x+1.5y≤5500
convert primal problem to dual problem
Min Zd=7000w1+4000w2+5500w3subject to 2w1+w2+2w3≥904w1+2.5w2+1.5w3≥110andw1,w2,w3≥0;
now we solve dual problem with BIG-M method
Min Z=7000w1+4000w2+5500w3+0w1+0w2+MA1+MA2subject to2w1+w2+2w3−w1+A1=904w1+2.5w2+1.5w3−w2+A2=110andw1,w2,w3,w1,w2,A1,A2≥0
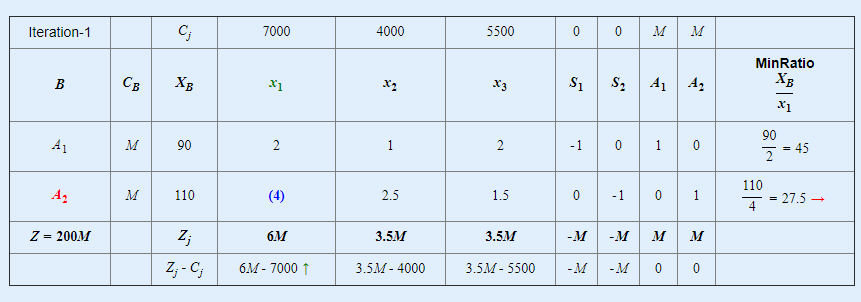
Positive max Zj−Cj is 6M−7000 and its column index is 1. So, the entering variable is w1.Minimum ratio is 27.5 and its row index is 2. So, the leaving basis variable is A2.∴ The pivot element is 4.Entering =w1, Departing =A2, Key Element =4
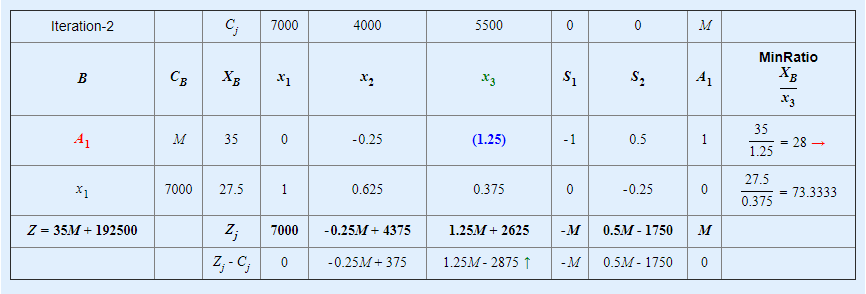
Positive max Zj−Cj is 1.25M−2875 and its column index is 3. So, the entering variable is w3.Minimum ratio is 28 and its row index is 1. So, the leaving basis variable is A1.∴ The pivot element is 1.25.Entering =w3, Departing =A1, Key Element =1.25
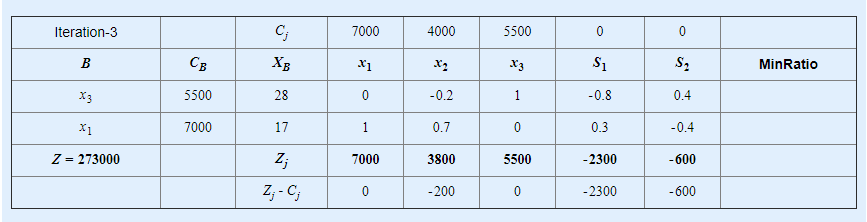
Since all Zj−Cj≤0Hence,optimal solution is arrived with value of variables as:w1=17,w2=0,w3=28MinZ=273000we can write solution for primal problem
maximum profit $273000 by making type T1 table 2300 and type T2 table 600


Comments