Question

State and prove ASASA for congruence of convex quadrilaterals.

Answer 1

Solution.

Theorem. If the vertices of two quadrilaterals are in one-to-one correspondence such that the three consecutive angles and two included sides of one quadrilateral are congruent to the corresponding angles and sides the other quadrilateral, then the quadrilaterals are congruent.

Proof.

Suppose quadrilaterals $ABCD$ and $A'B'C'D'$ are such that $\angle DAB \cong \angle D'A'B', \angle ABC \cong \angle A'B'C', \newline \angle BCD \cong \angle B'C'D', \overline{AB} \cong \overline{A'B'}$and $\overline{BC} \cong \overline{B'C'}.$ It must be shown that the quadrilateral $ABCD$ is congruent to the quadrilateral $A'B'C'D'.$ That it, by definition of congruence for quadrilaterals, it remains to establish that $\overline{AD} \cong \overline{A'D'}, \overline{CD} \cong \overline{C'D'}$ and $\angle CDA \cong \angle C'D'A'.$

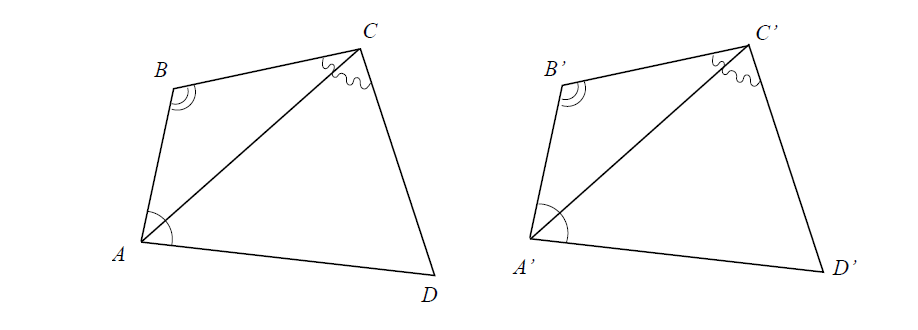
Draw the segments $\overline {AC}$ and $\overline {A'C'}$. Then by the SAS axiom $\triangle ABC \cong \triangle A'B'C'$. Therefor $\overline {AC} \cong \overline{A'C'}, \angle BAC \cong \angle B'A'C'$ and $\angle BCA \cong \angle B'C'A'$. By the angle addition axiom $m \angle CAD = m \angle BAD - m \angle BAC$ and $m \angle C'A'D' = m \angle B'A'D' - m \angle B'A'C'$. By assumption $m \angle BAD=m \angle B'A'D'$. It has been just concluded that $m \angle BAC = m \angle B'A'C'$. Therefor $m \angle CAD=m \angle C'A'D'$ and so $m \angle CAD \cong m \angle C'A'D'$.

Similarly, the angle addition axiom implies that $m \angle ACD=m \angle BCD-m \angle BCA=\newline =m \angle B'C'D'-m \angle B'C'A'=m \angle A'C'D'$, and so $\angle ACD \cong \angle A'C'D'.$ Therefor by the ASA Congruence Theorem for triangles $\triangle ACD \cong \triangle A'C'D'.$ This implies that $\overline {AD} \cong \overline {A'D'}, \overline {CD} \cong \overline {C'D'}$ and $\angle CDA \cong \angle C'D'A'.$

Thus the four sides and the four angles of ABCD are congruent to the corresponding sides and angles of $A'B'C'D'$ and hence the quadrilaterals $ABCD$ and $A'B'C'D'$ are congruent as required.