Question #6344
X is a Normed linear space. T is a function from X to X. Then T is a bounded linear transformation
Expert's answer
Not every linear operator between normed spaces is bounded. Let X be the space of all trigonometric polynomials defined on [−π, π], with the norm
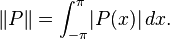
Define the operator L:X→X which acts by taking the derivative, so it maps a polynomial P to its derivative P′. Then, for
v = einx with n=1, 2, ...., we have while
while  as n→∞, so this operator is not bounded.
as n→∞, so this operator is not bounded.
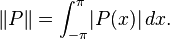
Define the operator L:X→X which acts by taking the derivative, so it maps a polynomial P to its derivative P′. Then, for
v = einx with n=1, 2, ...., we have
 while
while  as n→∞, so this operator is not bounded.
as n→∞, so this operator is not bounded.
Learn more about our help with Assignments: Functional Analysis


Comments