Question

Find the image of the upper half of the xy-plane under the square transformation w = z .

Answer 1

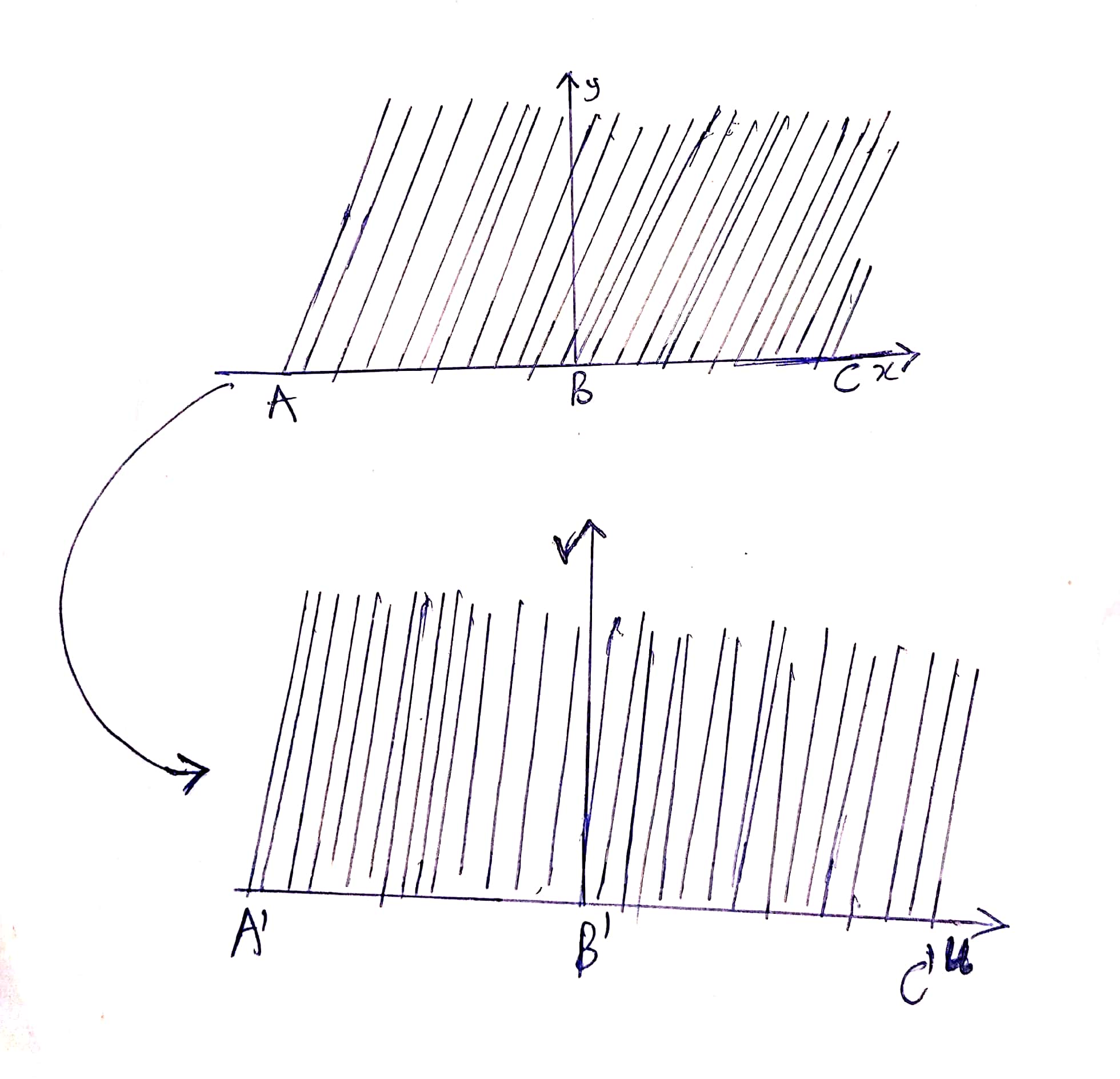
$\textsf{Let us apply the transformation}\, w = z \\ \textsf{to the shaded region}\\ \textsf{Then}\, w = u + jv = x + jy \\ \therefore u = x, \therefore v = y\\ \textsf{Now we map point}\, B \, \textsf{onto}\, B' \\ (1) B: x = 0, y = 0, \therefore B': u = 0, v = 0 \\ \textsf{We map the lines}\, AB \, \textsf{and} \, BC \\ \textsf{onto}\, A'B' \, \textsf{and} \, B'C' \, \textsf{in the}\, w\textsf{-plane.}\\ (a) AB: \textsf{As} \,x\textsf{-decreases from} -\infty \, \textsf{to}\, 0, u\textsf{-decreases from} \, -\infty\, \textsf{to}\, 0. \\ (b) BC: \textsf{As}\, x\textsf{-increases from}\, 0\, \textsf{to}\, \infty, u\textsf{-increases from} \, 0 \, \textsf{to}\, \infty. \\ \textsf{Finally, we can conclude that the shaded} \\ \textsf{region which is the upper half of the}\\ z\textsf{-plane maps onto to upper half of the}\, w\textsf{-plane.}$