Question

Find the volume in the first octant bounded by x+y+z=9, and the inside cylinder 3y=27-x^3

Answer 1

ANSWER : Volume= $\frac { 5589 }{ 70 } +4\sqrt { 3 } \quad \approx 79.84+6.93=86.77$

EXPLANATION

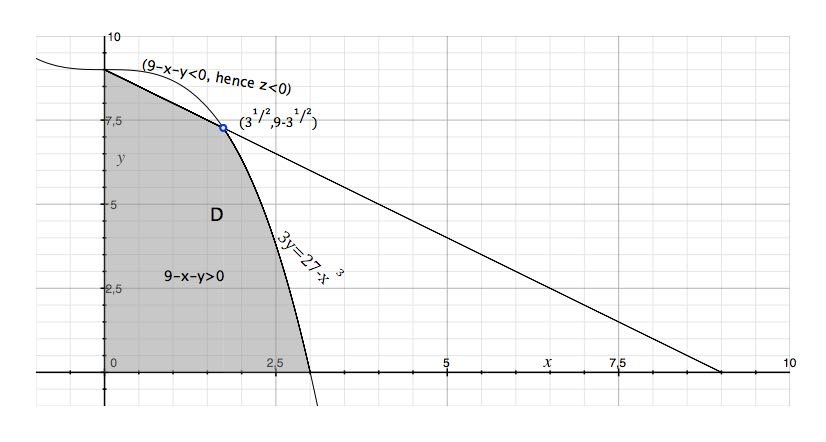
Denote by $W$ the region in the first octant bounded by $x+y+z=9$ and the inside cylinder $3y=27-\frac { { x }^{ 3 } }{ 3 }$ .

$Volume (W)=\iint _{ D }^{ \ }{ (9-x-y)dydx }$ , where $D={ D }_{ 1 }\cup { D }_{ 2 }\quad$, ${ D }_{ 1 }=\ \left\{ \left( x,y \right) :0\le x\le \sqrt { 3 } ,0\le y\le 9-x \right\} \ ,\\{ D }_{ 2 }=\ \left\{ \left( x,y \right) :\sqrt { 3 } \le x\le 3,\quad 0\le y\le 9-\frac { { x }^{ 3 } }{ 3 } \right\}.$

$\iint _{ { D }_{ 1 } }^{ \ }{ (9-x-y)dydx\ =\int _{ 0 }^{ \sqrt { 3 } }{ \left( \int _{ 0 }^{ 9-x }{ (\ 9-x } -y)dy \right) dx\quad = } }$ $=\int _{ 0 }^{ \sqrt { 3 } }{ \left[ { (9-x) }^{ 2 }-\frac { { (9-x) }^{ 2 } }{ 2 } \right] dx=\int _{ 0 }^{ \sqrt { 3 } }{ \left[ \frac { { (9-x) }^{ 2 } }{ 2 } \right] dx=\ { \left[ -\frac { { (9-x) }^{ 3 } }{ 6 } \right] }_{ 0 }^{ \sqrt { 3 } } } =\quad }$ $=\left[ -\frac { { (9-\sqrt { 3 } ) }^{ 3 } }{ 6 } \right] +\frac { { 9 }^{ 3 } }{ 6 }$ $=41\sqrt { 3 } -\frac { 27 }{ 2 }$ $=41\sqrt { 3 } -\frac { 945 }{ 70 }$ ,

$\iint _{ { D }_{ 2 } }^{ \ }{ (9-x-y)dydx\ =\ }$ $\int _{ \sqrt { 3 } }^{ 3 }{ \left( \int _{ 0 }^{ 9-\frac { { x }^{ 3 } }{ 3 } }{ (\ 9-x } -y)dy \right) dx\ = } \ \int _{ \sqrt { 3 } }^{ 3 }{ \left[ (9-x)\left( 9-\frac { { x }^{ 3 } }{ 3 } \right) -\frac { { \left( 9-\frac { { x }^{ 3 } }{ 3 } \right) }^{ 2 } }{ 2 } \right] } dx\ =$

$=\int _{ \sqrt { 3 } }^{ 3 }{ \left[ 81-9x-3{ x }^{ 3 }+\frac { { x }^{ 4 } }{ 3 } -\frac { 1 }{ 2 } \left( 81-6{ x }^{ 3 }+\frac { { x }^{ 6 } }{ 9 } \right) \right] } dx=$ ${ \left[ \frac { 81 }{ 2 } x-\frac { { 9x }^{ 2 } }{ 2 } +\frac { { x }^{ 5 } }{ 15 } -\frac { { x }^{ 7 } }{ 126 } \right] }_{ \sqrt { 3 } }^{ 3 }=$ $=\left( \frac { 243-81 }{ 2 } +\frac { 243 }{ 15 } -\frac { 2187 }{ 126 } \right) -\left( \frac { 81 }{ 2 } \sqrt { 3 } -\frac { 27 }{ 2 } +\frac { 3\sqrt { 3 } }{ \quad 5 } -\frac { 3\sqrt { 3 } }{ \quad 14 } \right) =$ $\ \frac { 3267 }{ 35 } \ -\frac { 1431 }{ 35 } \sqrt { 3 } .$

Therefore , $Volume (W)=\iint _{ D }^{ \ }{ (9-x-y)dydx } =$

$\iint _{ { D }_{ 1 } }^{ \ }{ (9-x-y)dydx+\iint _{ { D }_{ 1 } }^{ \ }{ (9-x-y)dydx \ = } }$

$=\ \frac { 5589 }{ 70 } +4\sqrt { 3 } \quad \approx 79.84+6.93=86.77\quad \quad$